OC : Optimisation et Commande

Présentation

Le groupe Optimisation et Commande s’intéresse aux mathématiques de la décision et étudie des systèmes de nature variée dans trois grands domaines de recherche qui sont l’optimisation, les systèmes dynamiques et les probabilités.
Le groupe développe des outils mathématiques, algorithmiques et logiciels permettant d'analyser, de commander et d'optimiser diverses classes de systèmes, y compris celles incluant des aspects dynamiques ou stochastiques. Ces développements font appel à plusieurs branches des mathématiques comme la théorie des graphes, la programmation mathématique, la géométrie différentielle, les systèmes dynamiques, l’analyse (convexe, non lisse, stochastique), l’algèbre linéaire, les probabilités, les processus stochastiques, ainsi que l'analyse numérique. Plusieurs de nos travaux sont à l’intersection de ces domaines.
Les applications traitées par le groupe sont nombreuses, et sont effectuées en collaboration avec des partenaires académiques et industriels diversifiés.

Mots-clés

Optimisation, systèmes dynamiques, probabilités.

Domaines d'applications

Systèmes cyber-physiques, énergie, transport, santé, logistique, planification, problèmes de réseaux, télécom, informatique quantique, contrôle optimal dans les applications aérospatiales, neurophysiologie, astrodynamique et gravitation, finance.

La suite présente les différents thèmes de recherche de l'équipe.

Optimisation continue, Systèmes dynamiques, Science des données

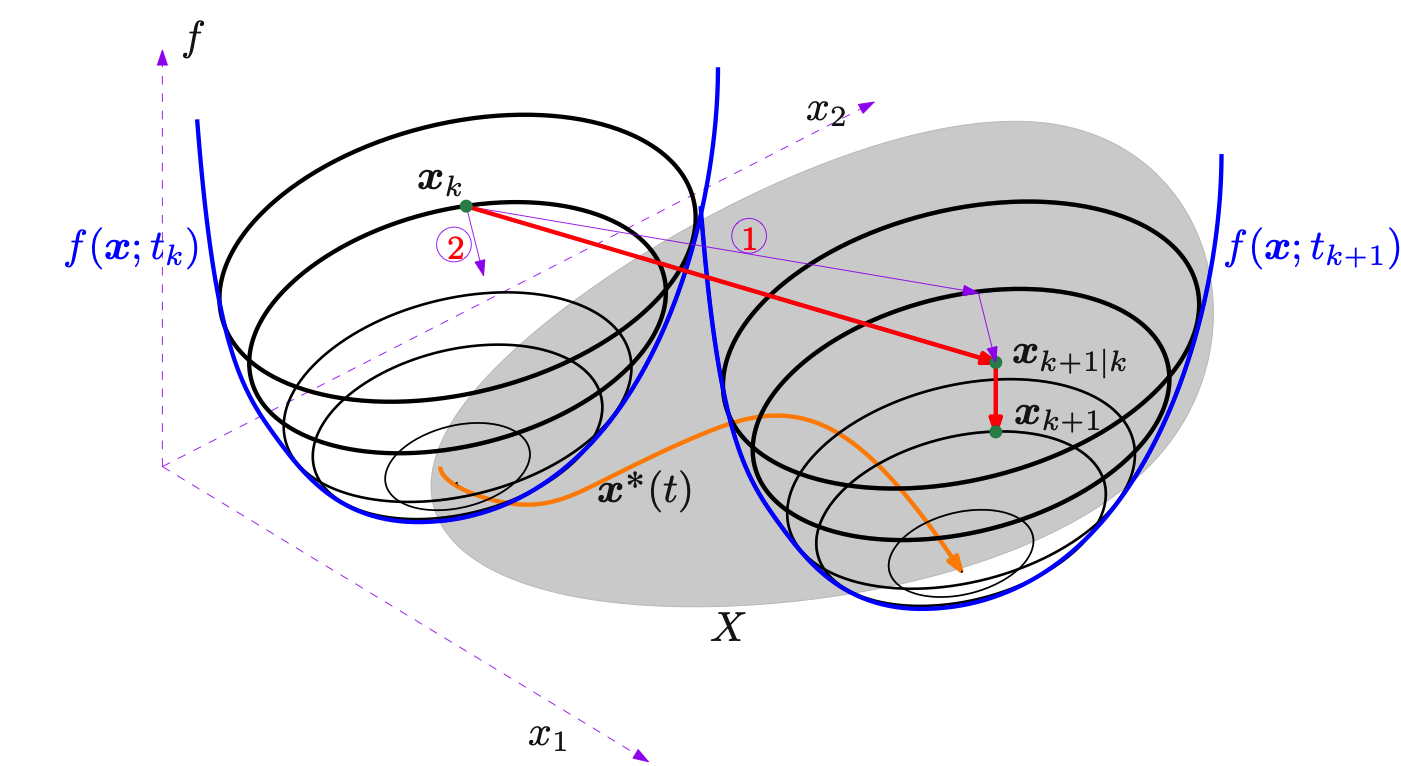
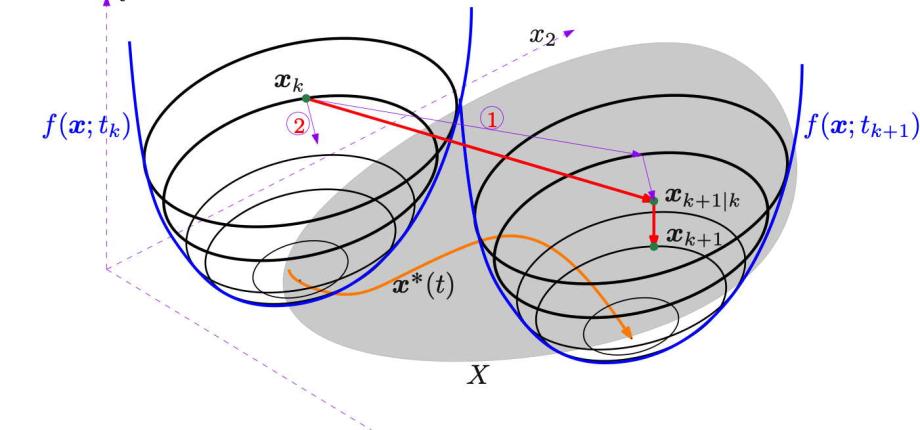
Les travaux dans ce domaine tournent autour de l'optimisation continue convexe, non convexe et vectorielle, en particulier dans la construction d'algorithmes du premier ordre pour résoudre des problèmes d’optimisation, éventuellement de grande dimension. Un soin particulier est apporté à l'examen des algorithmes du point de vue du système dynamique et aux cas dans lesquels les problèmes d'optimisation eux-mêmes changent avec le temps.
Récemment, nous explorons l'interaction entre l'optimisation et la science des données, en particulier pour les cas où le coût ou les contraintes doivent être déduits des données.

Mots clés

Optimisation convexe, méthodes de points proximaux, optimisation vectorielle, convexité généralisée, optimisation non lisse, algorithmes en ligne, optimisation variant dans le temps, apprentissage et préférences de l'utilisateur.

Applications

Systèmes cyber-physiques et sociaux (énergie, transport, santé), traitement du signal.

Optimisation Combinatoire, Recherche Opérationnelle, Sciences des données

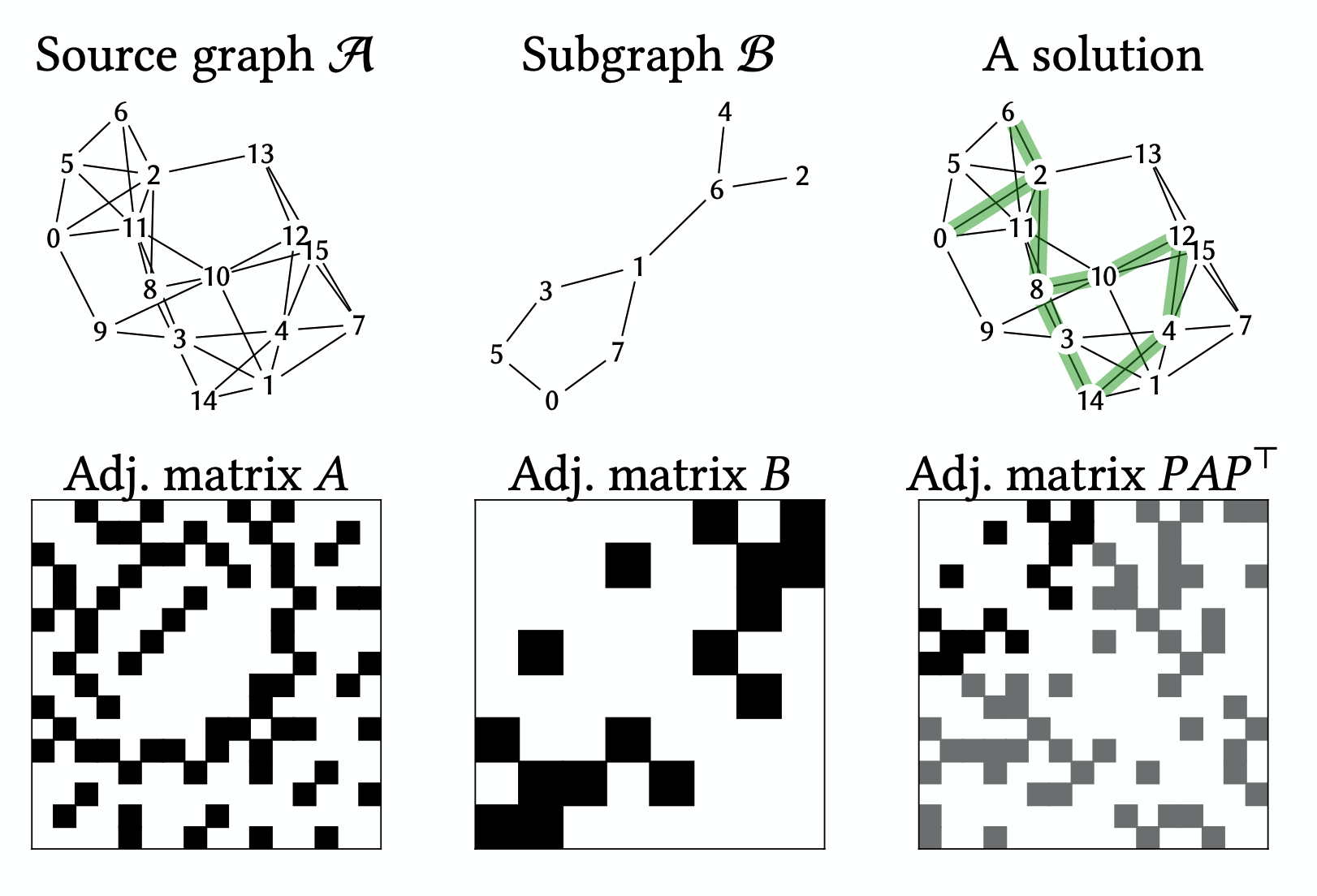
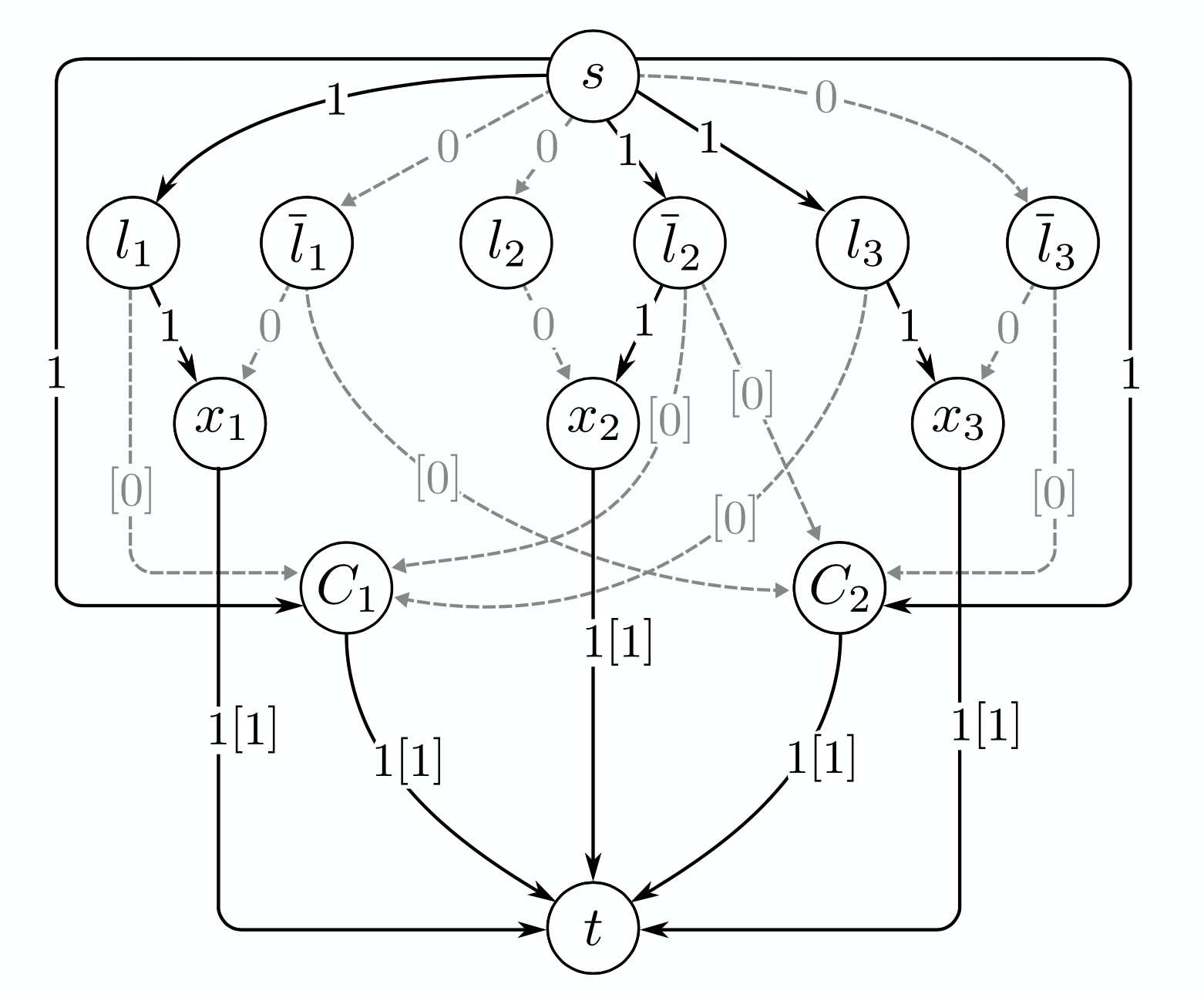
Les travaux dans ce domaine portent sur les techniques de formulation et de résolution de problèmes d'optimisation combinatoire (discrets) découlant d'applications de recherche opérationnelle. Ces problèmes sont généralement linéaires, quadratiques ou polynomiaux avec des variables de décision entières. Un soin particulier est apporté à la formulation et la reformulation des problèmes pour obtenir de meilleures garanties théoriques, à l'étude de la complexité, des algorithmes de décomposition (par exemple, branch-and-cut, Benders) et des heuristiques, ainsi qu'à la robustesse et la sensibilité de la solution aux changements de paramètres.

Récemment, nous explorons l'interaction entre l'optimisation combinatoire et la science des données, notamment lorsqu'elles peuvent s'entraider : en un sens, en proposant des certificats d'explicabilité de certains modèles d'apprentissage automatique, et inversement, afin d’apprendre comment optimiser la résolution de problèmes combinatoires. Très récemment, nous explorons l'interaction entre l'optimisation combinatoire et l'informatique quantique.
Nous avons un intérêt particulier pour les problèmes de conception ou de gestion de réseaux. On trouve ces problèmes par exemple dans les domaines de l’énergie, des transports, des télécommunications et de la défense.  

Mots clés

Optimisation combinatoire discrète, théorie de la complexité, problèmes d'optimisation en nombres entiers, optimisation linéaire, quadratique et polynomiale avec variables entières, QUBO, méthodes de décomposition, robustesse, apprendre à optimiser, arbres de décision.

Applications

Logistique, problèmes de réseau, planification, énergie et transports intelligents, télécom, analyse de texte, informatique quantique.

Systèmes dynamiques, Contrôle géométrique, Dynamique de l'univers

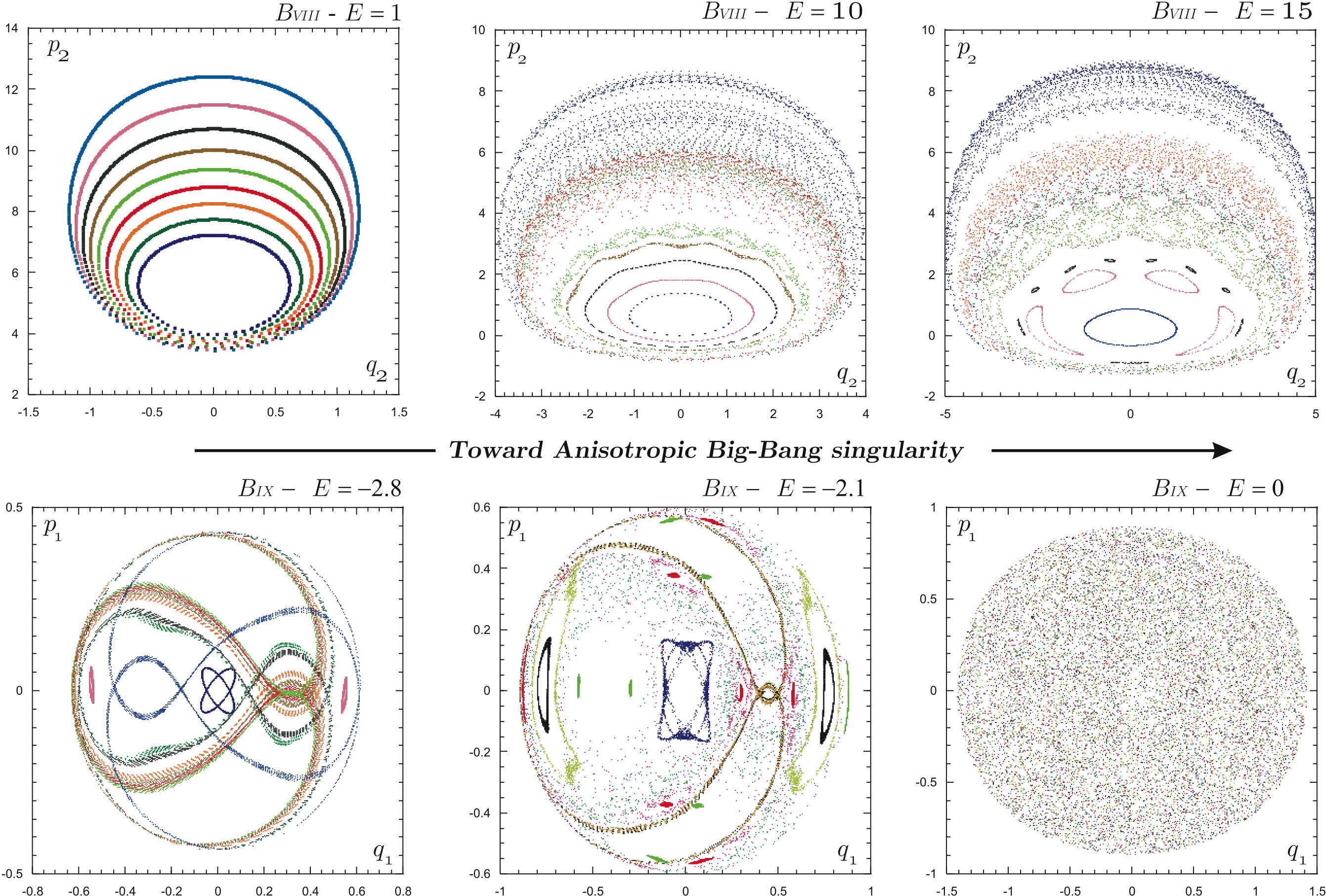
Les travaux dans ce domaine s'articulent autour de deux axes principaux : le contrôle géométrique et l'astrodynamique.

Sur le premier axe, nous nous intéressons à la théorie du contrôle non linéaire, et plus particulièrement au contrôle géométrique. Ici, l'objectif est d'aborder les problèmes de contrôle via la géométrie différentielle, avec un accent particulier sur la géométrie sous-riemannienne.

Sur le deuxième axe, nous nous intéressons aux systèmes dynamiques soumis aux lois gravitationnelles, avec un accent particulier sur la gravitation classique et relativiste, la dynamique des amas globulaires, des galaxies, la théorie des oscillations isochrones et la dynamique de l'univers entier.

Mots clés

Contrôle géométrique, géométrie sous-riemannienne, systèmes non-holonomes, problèmes de contrôle inverse, gravitation classique et relativiste, dynamique des amas globulaires et des galaxies, théorie des oscillations isochrones, dynamique de l'univers.

Applications

Contrôle optimal dans les applications aérospatiales (par exemple, rentrée de fusée), neurophysiologie, astrophysique.

Analyse stochastique et contrôle