OC: Optimisation and Control
The Optimisation and Control Group focuses on decision theory and in particular on three main research areas: optimisation, dynamical systems, and probability. The group develops theory, algorithms and software for the analysis, control and optimisation of various classes of systems, including dynamical and stochastic aspects. Its research is fundamentally rooted in several facets of mathematics, such as graph theory, mathematical programming, differential geometry, dynamical systems, (convex, non-smooth, and stochastic) analysis, linear algebra, probability, stochastic processes, and numerical methods. Several of our papers live at the intersection of these fields. The group also applies its results to many application domains, and its members have a wide range of academic and industrial collaborations.
Keywords: Optimisation, dynamical systems, probability.
Applications domains: cyber-physical systems, energy, transportation, health, logistics, planning, network problems, telecom, quantum computing, optimal control in aerospace application, neurophysiology, astrodynamics and gravitation, finance.
Continuous Optimization, Dynamical systems, Data science
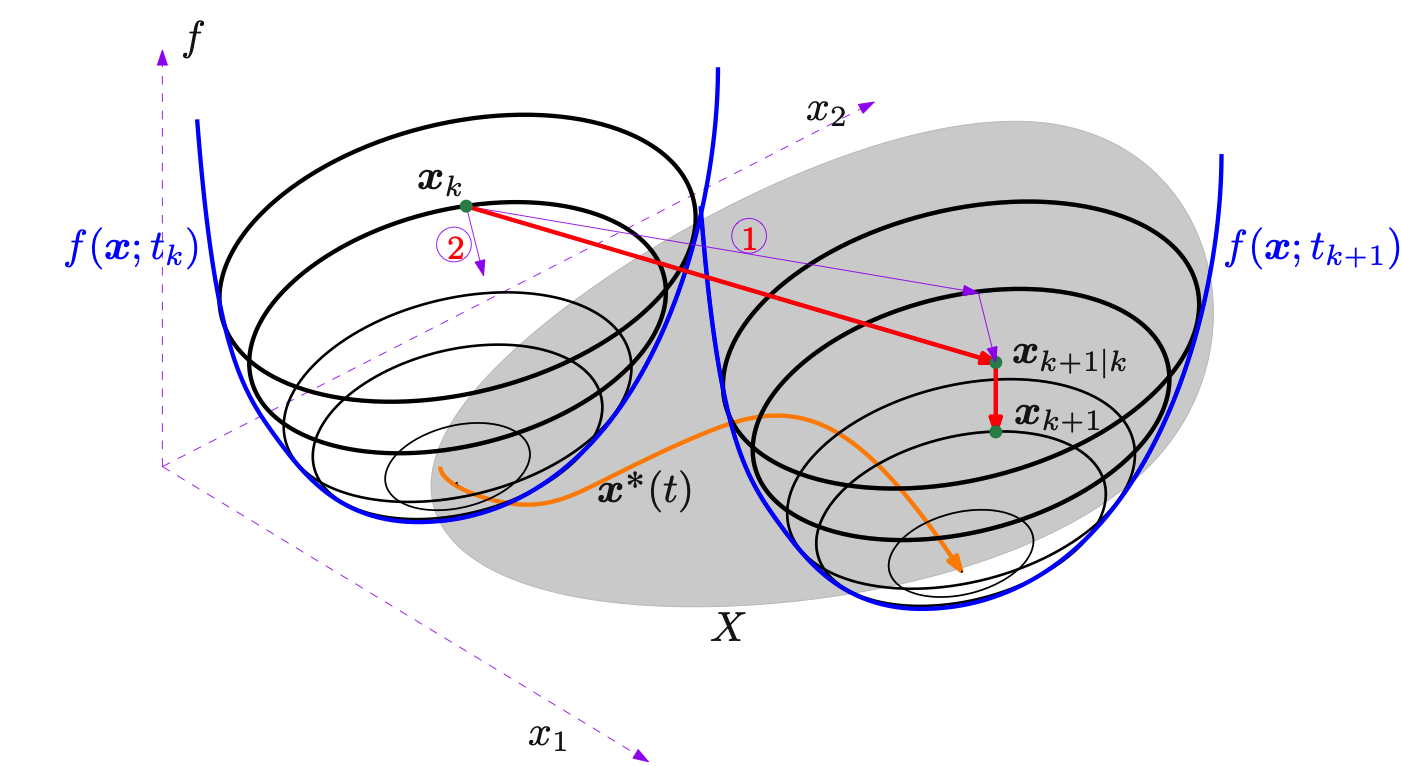
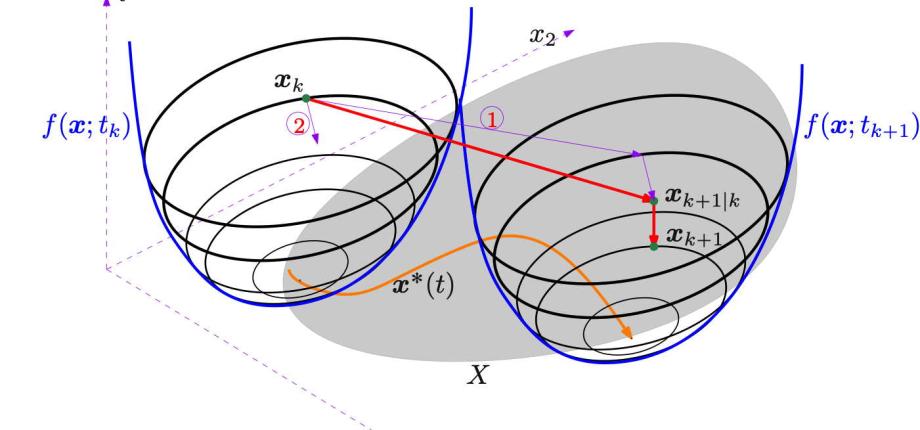
Work in this domain is centered around convex, non-convex and vector continuous optimisation, especially in the context of building first-order algorithms for the resolution of optimisation problems of possibly large dimension. Special emphasis is put into looking at the algorithms from a dynamical system perspective and at cases in which the optimisation problems themselves change over time.
Recently, we are exploring the interplay between optimisation and data science, especially for cases in which the cost or the constraints must be inferred from data.
Keywords
Convex optimisation, proximal point methods, vector optimization, generalised convexity, nonsmooth optimization, online algorithms, time-varying optimization, learning and user’s preferences.
Applications
Cyber-physical and social systems (energy, transportation, health), signal processing.
Combinatorial optimization, Operations Research, Data science
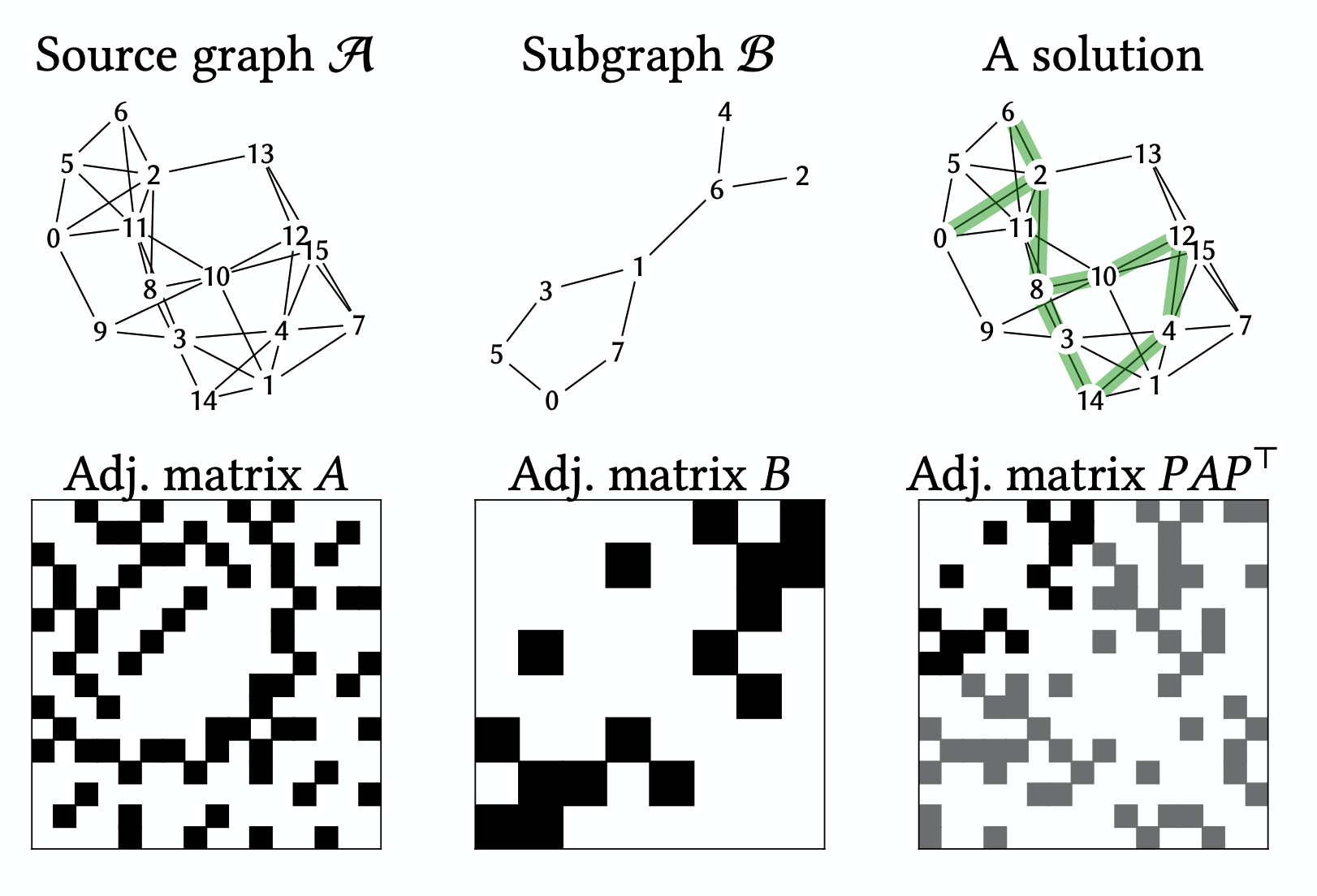
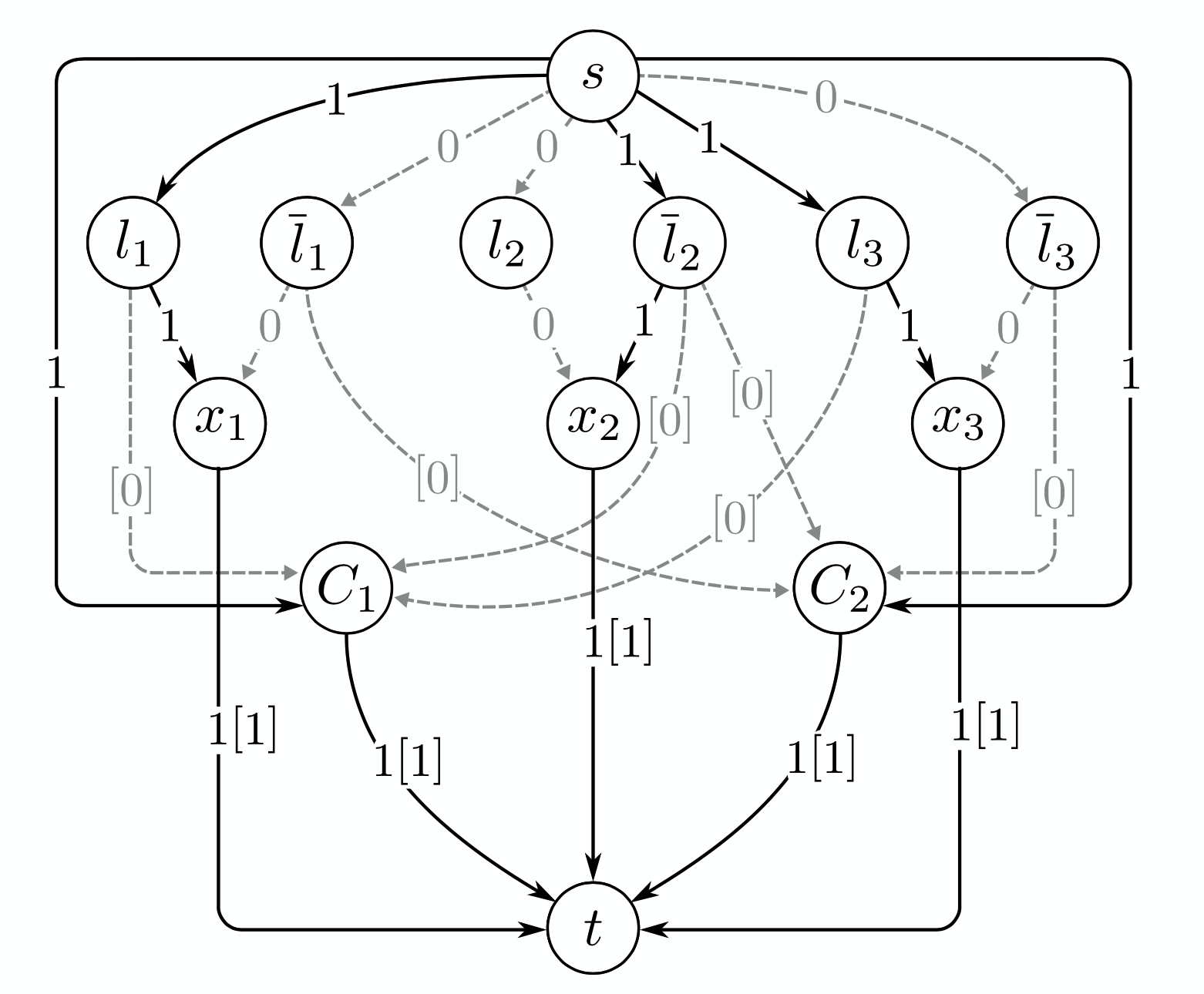
Work in this domain is centred around the formulation and resolution techniques for combinatorial (discrete) optimisation problems stemming from operations research applications. These problems are typically linear, quadratic, or polynomial optimisation problems with integer decision variables. Particular care is put in the formulation and re-formulation of problems to obtain better theoretical guarantees, the study of complexity, decomposition algorithms (e.g., branch and cut, Benders) and heuristics, as well as the robustness and sensitivity of the solution to parameter changes.
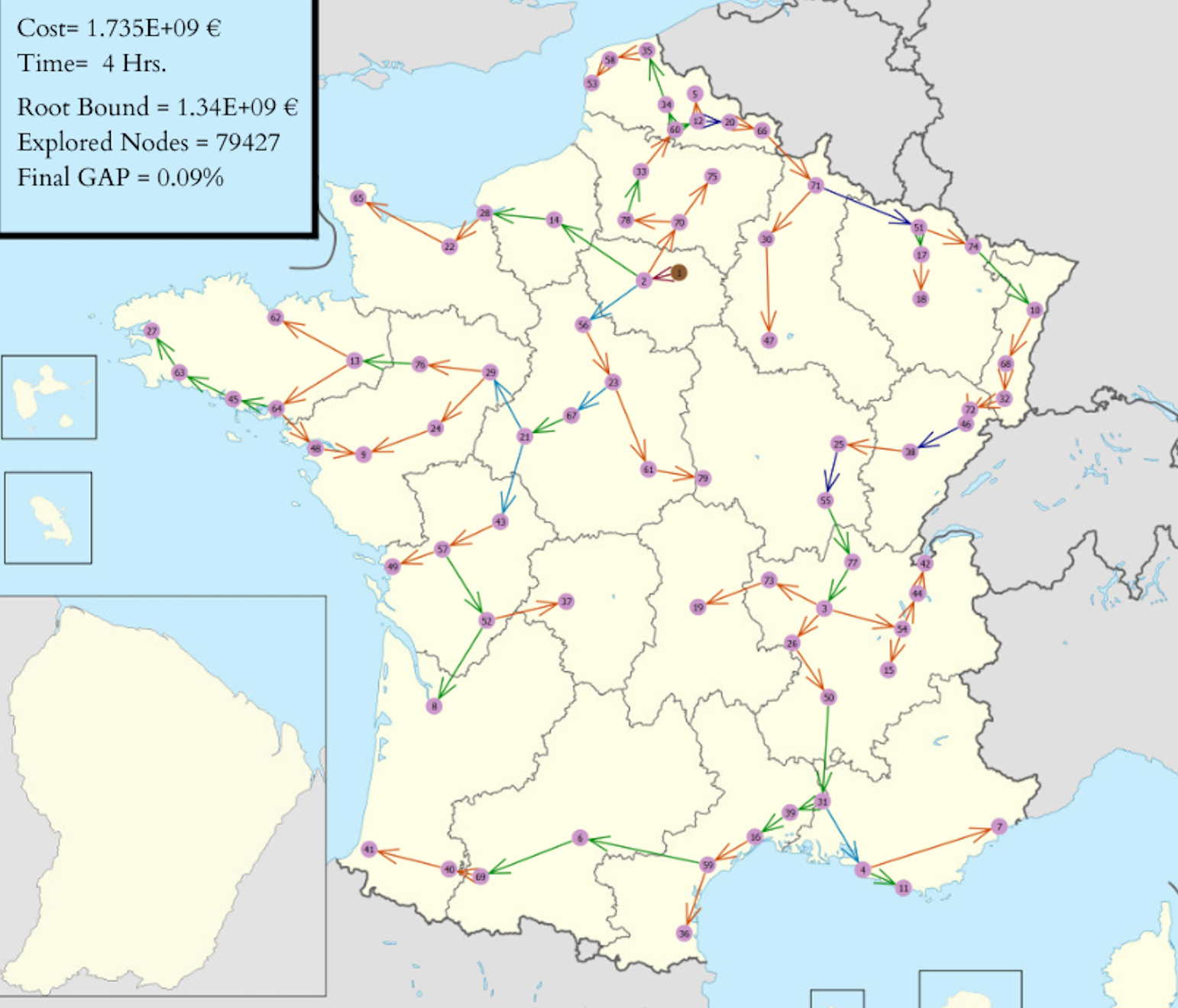 Recently, we are exploring the interplay between combinatorial optimisation and data science, especially when they can help one another: in one direction as offering certificates of explainability of certain machine learning models, and in the other direction as techniques to learn how to optimise hard combinatorial problems. Very recently, we are exploring the interplay between combinatorial optimisation and quantum computing.
Recently, we are exploring the interplay between combinatorial optimisation and data science, especially when they can help one another: in one direction as offering certificates of explainability of certain machine learning models, and in the other direction as techniques to learn how to optimise hard combinatorial problems. Very recently, we are exploring the interplay between combinatorial optimisation and quantum computing.
Keywords
Combinatorial discrete optimisation, complexity theory, integer optimisation problems, linear, quadratic, and polynomial optimisation with integer variables, QUBO, decomposition methods, robustness, learning to optimise, decision trees.
Applications
Logistics, network problems, planning, smart energy and transportation, telecom, text analysis, quantum computing.
Dynamical systems, Geometric control, Dynamics of the universe
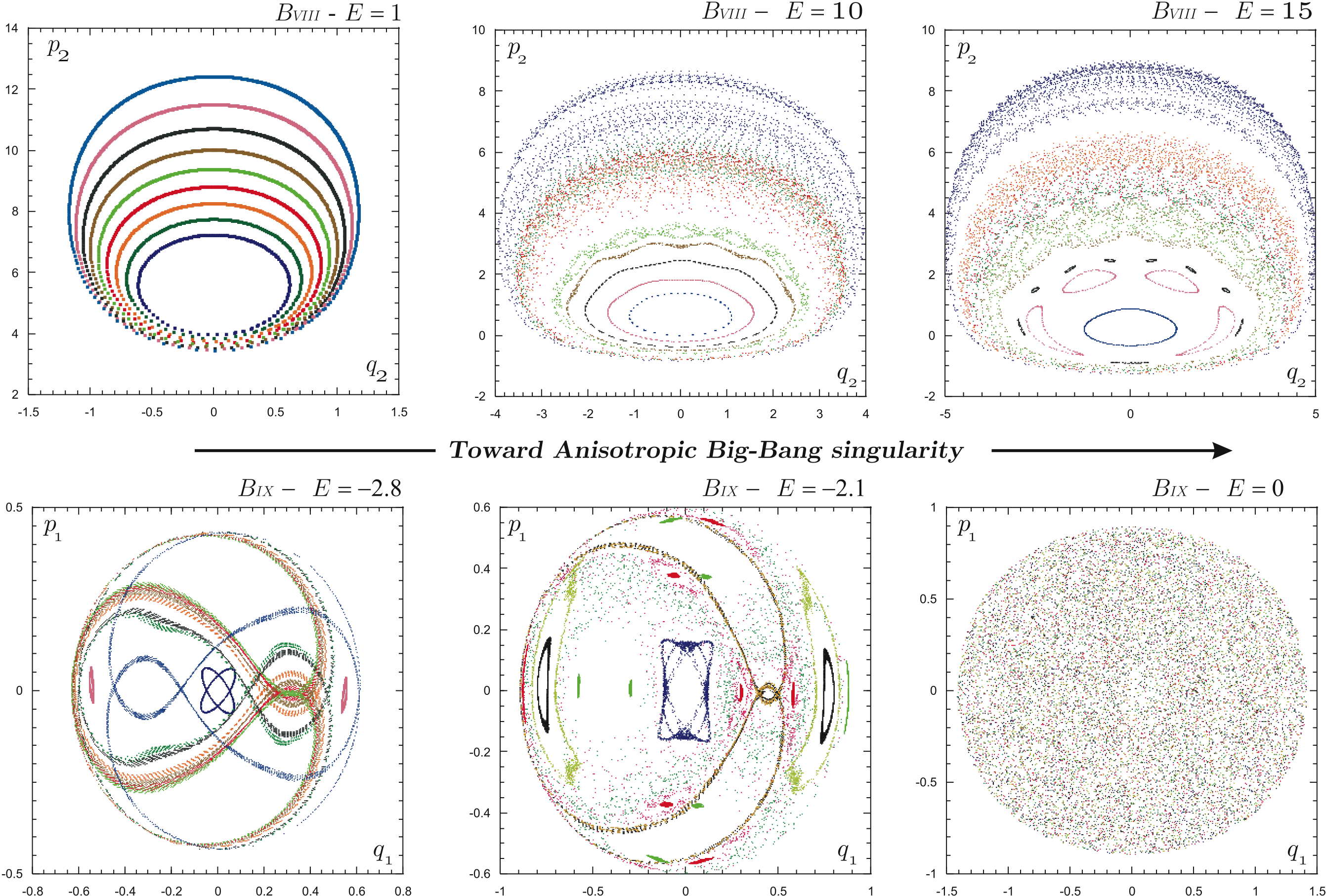
Work in this domain is centered around two main axes: geometric control and astrodynamics. For the former, we are interested in the theory of non-linear control, and specifically geometric control. Here the aim is to tackle control problems via differential geometry, with a special emphasis in sub-Riemannian geometry. For the latter, we are interested in dynamical systems under gravitational laws, with special emphasis to classical and relativistic gravitation, the dynamics of globular clusters, galaxies, the theory of isochrone oscillations, and the dynamics of the entire universe.
Keywords
Geometric control, sub-Riemannian geometry, non-holonomic systems, Inverse control problems, classical and relativistic gravitation, the dynamics of globular clusters, galaxies, the theory of isochrone oscillations, the dynamics of the universe.
Applications
Optimal control in aerospace application (e.g., rocket re-entry), neurophysiology, theoretical astrophysics.
Stochastic Analysis and Control
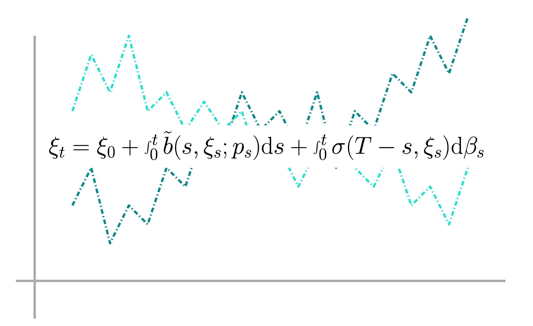
Work in this domain is based on different axes. The first is stochastic calculus via regularisation, with an eye to jump processes and infinite dimension often due to the non-Markovian character of the involved processes. Another axis is the probability representation of solutions of partial differential equations (PDEs) with irregular coefficients, as well as the related numerical methods. The third axis is centred around backward stochastic differential equations (BSDEs), for instance related to risk control, for example in quantitative finance with applications to financial markets, energy markets, and stochastic control with partial observation.
See Probabilités-Statistiques-Contrôle seminar.
Keywords
Stochastic calculus via regularisation, solutions of partial differential equations (PDEs) with irregular coefficients, risk control, stochastic control, backward stochastic differential equations (BSDEs).
Applications
Mathematical finance, mathematical physics.

